How do we differentiate between an item that is just over a complexity threshold and on that is, say, 10 times the threshold? The answer is normalization - we calculate a percentage from the value and the threshold as follows:

Max ( Value - Threshold, 0 )
Value

As an example, consider Fat for methods with a threshold of 15 (paths). Clearly a value less than or equal to the threshold will evaluate to 0% excess complexity, which is exactly as desired.

E.g. for value = 10: max( (10 - 15)/10, 0 ) = max( -0.5, 0 ) = 0

Values greater than the threshold evaluate to numbers that converge to, but never reach 100%.

E.g. value = 30: (30-15)/30 = 50%

E.g. value = 150: (150-15)/150 = 90%

The following chart shows the approximate shape of the normalization curve.

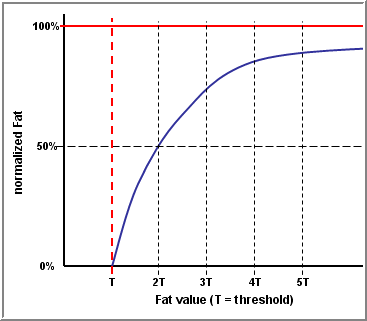
Effect of Fat normalization formula

The value of design tangle metric is already a percentage (with a range 0-50%), and we do not normalize it further.

In the case where a high-level package both exceeds the Fat threshold and is tangled, we add the normalized Fat value to the Tangled value to get an overall excess complexity value for the item.

Now we need to relate the excessive complexity of items at different levels of composition.